Før eller siden står hver forelder overfor problemet med hvordan man raskt lærer multiplikasjonstabellen. Mine egne minner fra denne perioden er allerede ganske uskarpe, men fortsatt ikke veldig hyggelige. Du må på en eller annen måte intrigere barnet, gjøre denne prosessen veldig morsom og forståelig. Synes du dette er fantastisk? Vi er uenige!
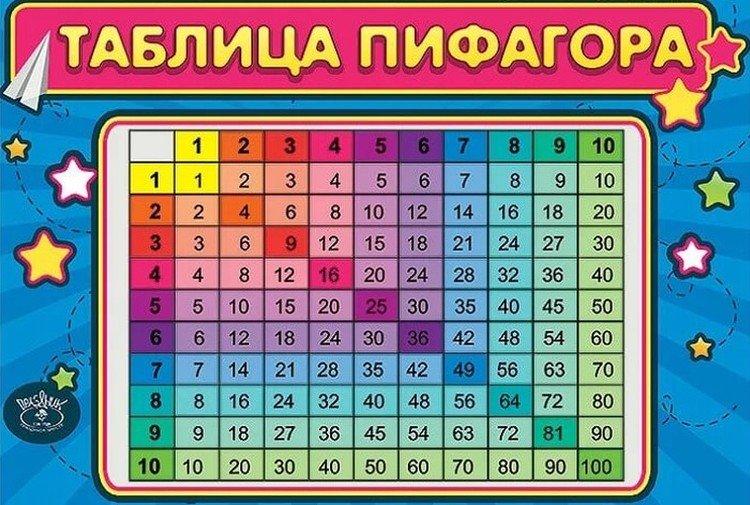
1. Pythagoras -bord i stedet for standard
Vi snakker om måten å skrive bordet på, og fra dette synspunktet vinner Pythagoras ubetinget. I stedet for en rekke usammenhengende linjer som "2x3 = 6", er det pytagoreiske bordet satt sammen til en firkant. Du må velge en multiplikator til venstre, og den andre på toppen, og finne skjæringspunktet deres. Jo mer visuelt demonstrerende materiale, jo bedre lærer barna det.
2. Permutasjon av faktorer
Forklar barnet ditt så tidlig som mulig at omorganisering av faktorene ikke endrer resultatet. For første gang sjokkerer og demotiverer det nye informasjonsmengden barnet. Men hvis du forstår at du faktisk må lære mye mindre der - det styrker godt!
3. Tellepinner
Tall skrevet på papir er abstrakte og ikke veldig klare saker for et barn. La ham operere med det han kan røre og utvide på egen hånd. Du vil se hvor mye lettere det er å lære at fra to hauger med tre pinner får du seks pinner, enn bare å huske et eksempel bak på en notatbok.
Hvordan lære et barn å lese: enkle måter og teknikker
4. Telle celler
Pinner og leker er nyttige når det gjelder små tall. Men selv 5x5 i dette formatet er allerede i ferd med å bli til et rot og kaos av ting. Da kommer cellene som må males over til unnsetning. La barnet telle ned fra ett punkt fem celler ned og fem til høyre, og deretter male over hele firkanten. Forresten, det er fra denne teknikken det er mest praktisk å bytte til det pytagoreiske torget.
5. Dikt og sanger
Morsomme rimlinjer huskes alltid bedre. Reglene for å lære språk for barn er basert på dette prinsippet. Og i matematikk kan den også brukes, så hent søte rim på internett eller skriv dem sammen med barnet ditt. Det er også en flott øvelse for å utvikle fantasi, fantasi og kreativitet.
6. Kort
I hvilke fag bruker de ikke kort med lyse bilder og store inskripsjoner. Det viktigste er at de er veldig interessante og liker barnet - og da vil han bygge assosiative forbindelser mye raskere og huske reglene.
I prosessen er det praktisk å legge til side de kortene som barnet ikke takler første gang, slik at de senere kan gjentas hver for seg. I fremtiden vil det være mulig å lære divisjon ved å bruke de samme kortene.
7. Spill og applikasjoner
Fra tidlig barndom er barna allerede mer profesjonelle enn foreldrene sine i å håndtere smarttelefoner og nettbrett. Det er mange applikasjoner nå som lar deg øve poengsummen din som et spill. Dette kan være en mer kjent og forståelig form for dagens førskolebarn og barneskoleelever.
8. Regularitet for de fem
For å multiplisere med 5 må du bare legge til fem hver gang. Det er praktisk å vurdere dette selv for de yngste matematikerne. Behandle barnet med partall og oddetall, og si at multiplisering av 5 med partall alltid gir resultatet med 0, og med oddetall - med 5.
Baldakin for barneseng (65 bilder): typer, hvordan å sy
9. Regelmessighet for de ni
Det er problemer med de ni, fordi du må operere med store tall. Men det er et morsomt mønster: hvis du skriver ned alle ligningene i rekkefølge fra 9x1 til 9x10, kan du finne en sekvens av de første og siste sifrene i svarene. Førstnevnte går opp fra 0, og sistnevnte går ned fra 9.
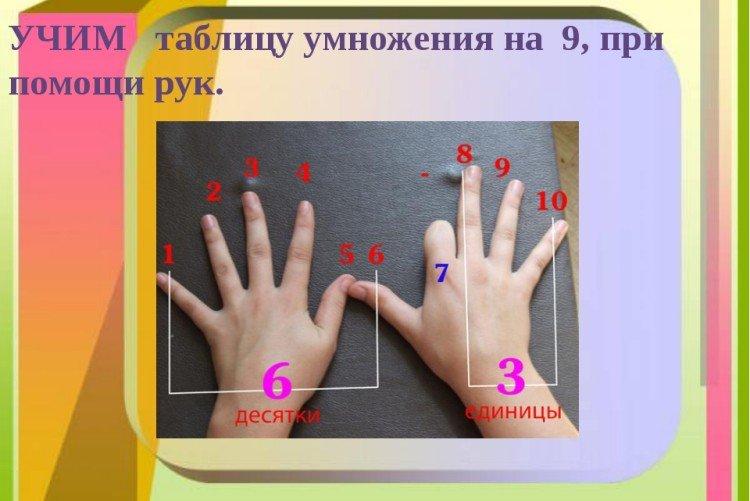
10. Fingre
Fingerprinsippet er en annen måte å håndtere de problematiske ni. Hvis du legger begge håndflatene på bordet og bøyer en finger, tilsvarer antallet fingre svarets sifre når du multipliserer det hevede tallet med 9.For eksempel, hvis du bøyer den 6. fingeren, forblir 5 foran den, og etter den - 4, totalt - 6x9 = 54.
