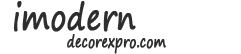Vroeg of laat wordt elke ouder geconfronteerd met het probleem om snel de tafel van vermenigvuldiging te leren. Mijn eigen herinneringen aan deze periode zijn al wat wazig, maar nog steeds niet erg prettig. Je moet het kind op de een of andere manier intrigeren, dit proces echt leuk en begrijpelijk maken. Vind je dit fantastisch? We zijn het er niet mee eens!
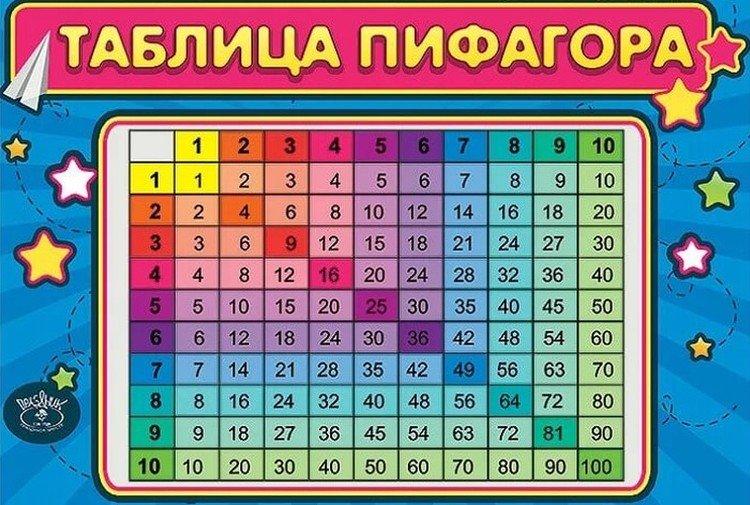
1. Pythagoras-tafel in plaats van standaard
We hebben het over de manier van tafelschrijven en vanuit dit oogpunt wint Pythagoras onvoorwaardelijk. In plaats van een reeks onsamenhangende lijnen zoals "2x3 = 6", is de pythagorische tafel samengevoegd tot een vierkant. Je moet een vermenigvuldiger aan de linkerkant en de tweede aan de bovenkant kiezen en hun snijpunt vinden. Hoe meer visueel demonstratief materiaal, hoe beter de kinderen het leren.
2. Permutatie van factoren
Leg uw kind zo vroeg mogelijk uit dat het herschikken van de factoren het resultaat niet verandert. Voor het eerst schokt en demotiveert de nieuwe hoeveelheid informatie het kind. Maar als je begrijpt dat je daar in feite veel minder hoeft te leren - het stimuleert goed!
3. Telstokjes
Cijfers op papier zijn abstract en niet erg duidelijk voor een kind. Laat hem werken met wat hij zelf kan aanraken en uitbreiden. Je zult zien hoeveel gemakkelijker het is om te leren dat je van twee stapels van drie stokjes zes stokjes krijgt, dan alleen maar een voorbeeld uit het hoofd te leren van de achterkant van een notitieboekje.
Een kind leren lezen: eenvoudige manieren en technieken
4. Cellen tellen
Stokjes en speelgoed zijn handig als het om kleine aantallen gaat. Maar zelfs 5x5 in dit formaat verandert al in een puinhoop en chaos van dingen. Dan komen de cellen die overschilderd moeten worden te hulp. Laat het kind vanaf één punt vijf cellen naar beneden en vijf naar rechts aftellen en dan over het hele vierkant schilderen. Trouwens, het is van deze techniek dat het het handigst is om over te schakelen naar het Pythagoras-plein.
5. Gedichten en liedjes
Grappige rijmende regels worden altijd beter onthouden. De regels voor het leren van talen voor kinderen zijn gebaseerd op dit principe. En in de wiskunde kan het ook worden gebruikt, dus zoek leuke rijmpjes op internet of schrijf ze samen met je kind. Het is ook een geweldige oefening voor het ontwikkelen van fantasie, verbeeldingskracht en creativiteit.
DIY babyboek: 5 geweldige ideeën
6. Kaarten
Alleen in welke vakken gebruiken ze geen kaarten met heldere afbeeldingen en grote inscripties. Het belangrijkste is dat ze echt interessant zijn en van het kind houden - en dan zal hij veel sneller associatieve verbindingen opbouwen en de regels onthouden.
Daarbij is het handig om die kaarten die het kind de eerste keer niet aankan, opzij te leggen, zodat ze later afzonderlijk kunnen worden herhaald. In de toekomst zal het mogelijk zijn om met dezelfde kaarten te leren delen.
7. Games en applicaties
Van jongs af aan zijn kinderen al professioneler dan hun ouders in het omgaan met smartphones en tablets. Er zijn nu veel toepassingen waarmee u uw score als een spel kunt oefenen. Dit is misschien een meer bekende en begrijpelijke vorm voor de kleuters en basisschoolleerlingen van vandaag.
8. Regelmaat voor de vijf
Om met 5 te vermenigvuldigen, hoef je alleen maar vijf op te tellen. Het is handig om dit zelfs voor de jongste wiskundigen te overwegen. Behandel het kind in even en oneven getallen, en zeg dat het vermenigvuldigen van 5 met even het resultaat altijd met 0 geeft, en met oneven - met 5.
Luifel voor een kinderbedje (65 foto's): soorten, hoe te naaien
9. Regelmaat voor de negen
Er zijn problemen met de negen, omdat je met grote aantallen moet werken. Maar er is een grappig patroon: als je alle vergelijkingen in de volgorde van 9x1 tot 9x10 opschrijft, kun je een reeks van de eerste en laatste cijfers van de antwoorden vinden. De eerste gaan omhoog vanaf 0 en de laatste gaan omlaag vanaf 9.
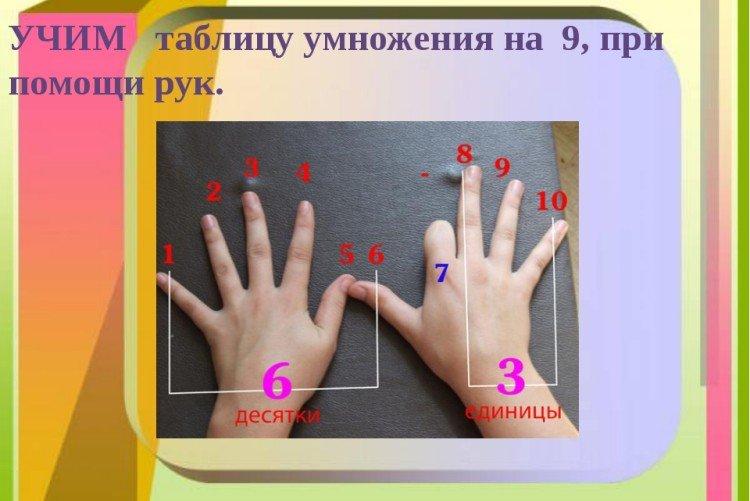
10. Vingers
Het vingerprincipe is een andere manier om met de problematische negen om te gaan. Als je beide handpalmen op tafel legt en een willekeurige vinger buigt, komt het aantal vingers overeen met de cijfers van het antwoord wanneer je het verhoogde getal met 9 vermenigvuldigt.Als u bijvoorbeeld de 6e vinger buigt, blijft er 5 voor over en daarna - 4, totaal - 6x9 = 54.
