Αργά ή γρήγορα, κάθε γονέας αντιμετωπίζει το πρόβλημα του πώς να μάθει γρήγορα τον πίνακα πολλαπλασιασμού. Οι δικές μου αναμνήσεις αυτής της περιόδου είναι ήδη μάλλον θολές, αλλά ακόμα όχι πολύ ευχάριστες. Πρέπει με κάποιο τρόπο να ιντριγκάρεις το παιδί, να κάνεις αυτή τη διαδικασία πραγματικά διασκεδαστική και κατανοητή. Πιστεύετε ότι αυτό είναι φανταστικό; Διαφωνούμε!
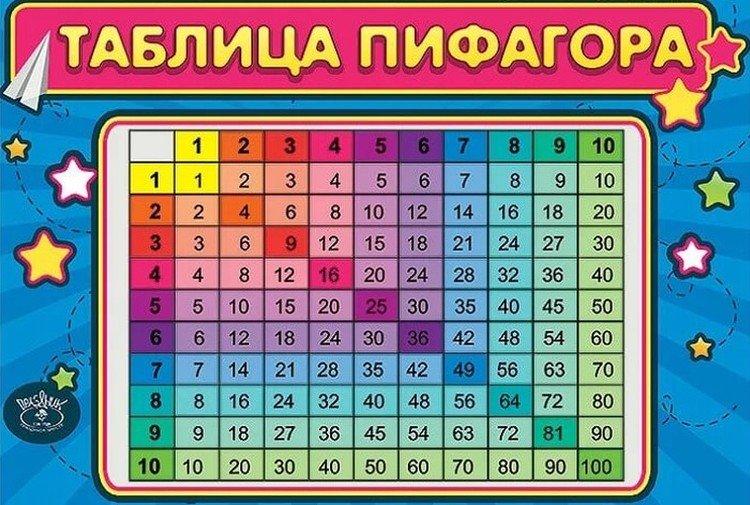
1. Πυθαγόρας τραπέζι αντί για στάνταρ
Μιλάμε για τον τρόπο γραφής του πίνακα, και από αυτή την άποψη, ο Πυθαγόρας κερδίζει άνευ όρων. Αντί για μια σειρά ασυνάρτητων γραμμών όπως "2x3 = 6", ο Πυθαγόρειος πίνακας συγκεντρώνεται σε ένα τετράγωνο. Πρέπει να επιλέξετε έναν πολλαπλασιαστή στα αριστερά και τον δεύτερο στην κορυφή και να βρείτε το σημείο τομής τους. Όσο πιο οπτικά επιδεικτικό υλικό, τόσο καλύτερα τα παιδιά το μαθαίνουν.
2. Μετάθεση παραγόντων
Εξηγήστε στο παιδί σας όσο το δυνατόν νωρίτερα ότι η αναδιάταξη των παραγόντων δεν αλλάζει το αποτέλεσμα. Για πρώτη φορά, ο νέος όγκος πληροφοριών συγκλονίζει και αποθαρρύνει το παιδί. Αλλά αν καταλάβετε ότι στην πραγματικότητα θα πρέπει να μάθετε πολύ λιγότερο εκεί - αναζωογονεί καλά!
3. Μετρώντας ραβδιά
Οι αριθμοί που γράφονται σε χαρτί είναι αφηρημένοι και δεν είναι πολύ ξεκάθαροι για ένα παιδί. Αφήστε τον να λειτουργήσει με αυτό που μπορεί να αγγίξει και να επεκταθεί μόνος του. Θα δείτε πόσο πιο εύκολο είναι να μάθετε ότι από δύο σωρούς από τρία μπαστούνια παίρνετε έξι μπαστούνια, παρά απλώς να απομνημονεύσετε ένα παράδειγμα από το πίσω μέρος ενός σημειωματάριου.
Πώς να μάθετε ένα παιδί να διαβάζει: απλοί τρόποι και τεχνικές
4. Καταμέτρηση κελιών
Τα μπαστούνια και τα παιχνίδια είναι βολικά όταν πρόκειται για μικρούς αριθμούς. Αλλά ακόμα και το 5x5 σε αυτή τη μορφή μετατρέπεται ήδη σε χάος και χάος πραγμάτων. Στη συνέχεια, τα κελιά που πρέπει να βαφτούν έρχονται στη διάσωση. Αφήστε το παιδί να μετρήσει αντίστροφα από ένα σημείο πέντε κύτταρα προς τα κάτω και πέντε προς τα δεξιά και, στη συνέχεια, ζωγραφίστε σε ολόκληρο το τετράγωνο. Παρεμπιπτόντως, από αυτήν την τεχνική είναι πιο βολικό να μεταβείτε στην πλατεία Πυθαγόρειου.
5. Ποιήματα και τραγούδια
Οι αστείες ομοιοκαταληξίες γραμμές θυμούνται πάντα καλύτερα. Οι κανόνες για την εκμάθηση γλωσσών για παιδιά βασίζονται σε αυτήν την αρχή. Και στα μαθηματικά, μπορεί επίσης να χρησιμοποιηθεί, οπότε πάρτε χαριτωμένες ρίμες στο Διαδίκτυο ή γράψτε τις μαζί με το παιδί σας. Είναι επίσης μια εξαιρετική άσκηση για την ανάπτυξη της φαντασίας, της φαντασίας και της δημιουργικότητας.
DIY μωρό βιβλίο: 5 υπέροχες ιδέες
6. Κάρτες
Σε ποια θέματα μόνο δεν χρησιμοποιούν κάρτες με φωτεινές εικόνες και μεγάλες επιγραφές. Το κύριο πράγμα είναι ότι είναι πραγματικά ενδιαφέροντα και σαν το παιδί - και στη συνέχεια θα δημιουργήσει συνειρμικές συνδέσεις πολύ πιο γρήγορα και θα απομνημονεύσει τους κανόνες.
Κατά τη διαδικασία, είναι βολικό να αφήσετε στην άκρη εκείνες τις κάρτες που το παιδί δεν αντιμετωπίζει την πρώτη φορά, έτσι ώστε αργότερα να μπορούν να επαναληφθούν ξεχωριστά. Στο μέλλον, χρησιμοποιώντας τις ίδιες κάρτες, θα είναι δυνατή η εκμάθηση της διαίρεσης.
7. Παιχνίδια και εφαρμογές
Από την παιδική ηλικία, τα παιδιά είναι ήδη πιο επαγγελματικά από τους γονείς τους στο χειρισμό smartphone και tablet. Υπάρχουν πολλές εφαρμογές τώρα που σας επιτρέπουν να εξασκήσετε τη βαθμολογία σας ως παιχνίδι. Αυτή μπορεί να είναι μια πιο οικεία και κατανοητή μορφή για τα σημερινά παιδιά προσχολικής ηλικίας και μαθητές δημοτικού.
8. Κανονικότητα για τα πέντε
Για να πολλαπλασιάσετε με 5, απλά πρέπει να προσθέσετε πέντε κάθε φορά. Είναι βολικό να το λάβουμε υπόψη ακόμη και για τους νεότερους μαθηματικούς. Αντιμετωπίστε το παιδί σε ζυγούς και περιττούς αριθμούς και πείτε ότι ο πολλαπλασιασμός του 5 με ζυγό δίνει πάντα το αποτέλεσμα με 0 και με το περιττό με το 5.
Κουβούκλιο για κούνια (65 φωτογραφίες): τύποι, πώς να ράβετε
9. Κανονικότητα για τους εννέα
Υπάρχουν προβλήματα με τα εννέα, επειδή πρέπει να λειτουργήσετε με μεγάλους αριθμούς. Υπάρχει όμως ένα αστείο μοτίβο: αν γράψετε όλες τις εξισώσεις με σειρά από 9x1 έως 9x10, μπορείτε να βρείτε μια ακολουθία από το πρώτο και το τελευταίο ψηφίο των απαντήσεων. Το πρώτο ανεβαίνει από το 0 και το δεύτερο κατεβαίνει από το 9.
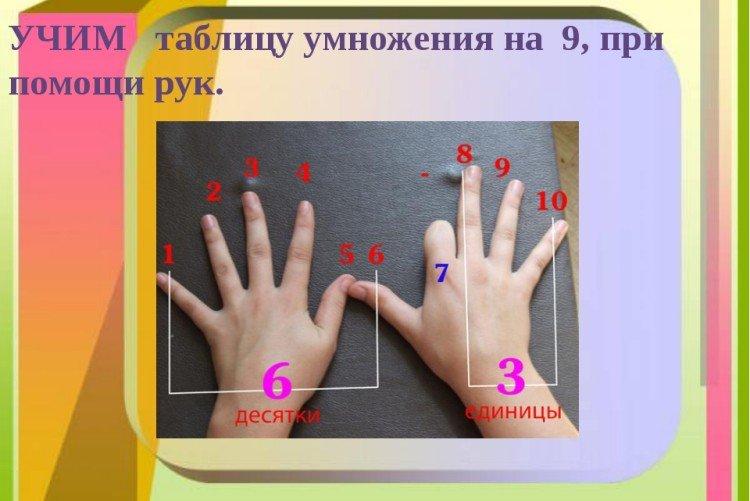
10. Δάχτυλα
Η αρχή του δακτύλου είναι ένας άλλος τρόπος αντιμετώπισης του προβληματικού εννέα. Εάν τοποθετήσετε και τις δύο παλάμες στο τραπέζι και λυγίσετε οποιοδήποτε δάχτυλο, τότε ο αριθμός των δακτύλων αντιστοιχεί στα ψηφία της απάντησης κατά τον πολλαπλασιασμό του αυξημένου αριθμού επί 9.Για παράδειγμα, εάν λυγίσετε το 6ο δάχτυλο, 5 παραμένουν πριν από αυτό και μετά από αυτό - 4, συνολικά - 6x9 = 54.
